Answer:
C. 7 units
Explanation:
The given parameters are;
The length of the chord of the circle,
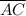 = 14 units
= 14 units
The orientation of the radius and the chord = The radius is perpendicular to the chord
We have in ΔAOC,
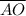 =
=
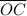 = The radius of the circle
= The radius of the circle
 ≅
≅
 by reflexive property
by reflexive property
The angle at point B = 90° by angle formed by the radius which is perpendiclar to the chord
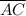
ΔAOB and ΔCOB are right triangles (triangles having one 90° angle)
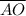 and
and
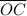 are hypotenuse sides of ΔAOB and ΔCOB respectively and
are hypotenuse sides of ΔAOB and ΔCOB respectively and
 is a leg to ΔAOB and ΔCOB
is a leg to ΔAOB and ΔCOB
Therefore;
ΔAOB ≅ ΔCOB, by Hypotenuse Leg rule of congruency
Therefore;
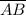 ≅
≅
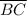 by Congruent Parts of Congruent Triangles are Congruent, CPCTC
by Congruent Parts of Congruent Triangles are Congruent, CPCTC
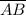 =
=
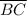 by definition of congruency
by definition of congruency
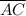 =
=
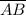 +
+
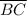 by segment addition postulate
by segment addition postulate
∴
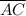 =
=
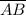 +
+
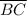 =
=
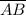 +
+
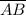 = 2 ×
= 2 ×
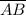
∴
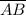 =
=
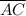 /2
/2
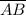 = 14/2 = 7
= 14/2 = 7
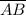 = 7 units.
= 7 units.