Answer:
Explanation:
This is the problem we need to solve:
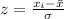 and we have everything but the z-score (which we find from a table) with our main unknown being the standard deviation.
and we have everything but the z-score (which we find from a table) with our main unknown being the standard deviation.
If the probability that a random variable that is less than 11 is .67, we first have to find the z-score from the table that is closest to .67, and there are 2:
P(z < .43) = .66640 and P(z < .44) = .67003
We'll use z = .44
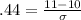 and
and
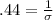 and
and
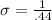 so
so
σ = 2.27 (check it; it works!)