Question

A power cycle receives QH by heat transfer from a hot reservoir at TH = 1200 K and rejects energy QC by heat transfer to a cold reservoir at TC = 400 K. For each of the following cases, determine whether the cycle operates reversibly, operates irreversibly, or is impossible.

a.QH = 900 kJ, Wcycle= 450 kJ
b. QH = 900 kJ, Qc = 300 kJ
c. Weycle = 600 kJ, Qc= 400 kJ
d. η = 75%

Answer 1

a) Irreversible, b) Reversible, c) Irreversible, d) Impossible.

Step-by-step explanation:

Maximum theoretical efficiency for a power cycle (
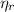`\eta_(r)`), no unit, is modelled after the Carnot Cycle, which represents a reversible thermodynamic process:

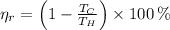`\eta_(r) = \left(1-(T_(C))/(T_(H)) \right)* 100\,\%` (1)

Where:

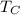`T_(C)` - Temperature of the cold reservoir, in Kelvin.

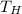`T_(H)` - Temperature of the hot reservoir, in Kelvin.

The maximum theoretical efficiency associated with this power cycle is: (
`T_(C) = 400\,K`,
`T_(H) = 1200\,K`)

`\eta_(r) = \left(1-(400\,K)/(1200\,K) \right)* 100\,\%`

`\eta_(r) = 66.667\,\%`

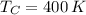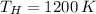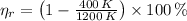
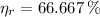
In exchange, real efficiency for a power cycle (
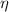`\eta`), no unit, is defined by this expression:

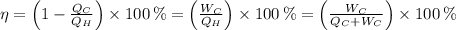`\eta = \left(1-(Q_(C))/(Q_(H))\right) * 100\,\% = \left((W_(C))/(Q_(H)) \right)* 100\,\% = \left((W_(C))/(Q_(C) + W_(C)) \right)* 100\,\%` (2)

Where:

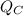`Q_(C)` - Heat released to cold reservoir, in kilojoules.

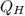`Q_(H)` - Heat gained from hot reservoir, in kilojoules.

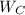`W_(C)` - Power generated within power cycle, in kilojoules.

A power cycle operates irreversibly for
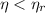`\eta < \eta_(r)`, reversibily for
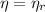`\eta = \eta_(r)` and it is impossible for
`\eta > \eta_(r)`.

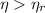Now we proceed to solve for each case:

a)
`Q_(H) = 900\,kJ`,
`W_(C) = 450\,kJ`

`\eta = \left((450\,kJ)/(900\,kJ) \right)* 100\,\%`

`\eta = 50\,\%`

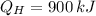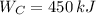
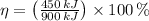
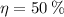
Since
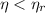`\eta < \eta_(r)`, the power cycle operates irreversibly.

b)
`Q_(H) = 900\,kJ`,
`Q_(C) = 300\,kJ`

`\eta = \left(1-(300\,kJ)/(900\,kJ) \right)* 100\,\%`

`\eta = 66.667\,\%`

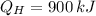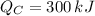
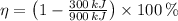
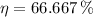
Since
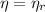`\eta = \eta_(r)`, the power cycle operates reversibly.

c)
`W_(C) = 600\,kJ`,
`Q_(C) = 400\,kJ`

`\eta = \left((600\,kJ)/(600\,kJ + 400\,kJ) \right)* 100\,\%`

`\eta = 60\,\%`

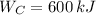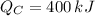
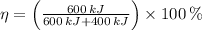
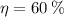
Since
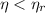`\eta < \eta_(r)`, the power cycle operates irreversibly.

d) Since
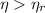`\eta > \eta_(r)`, the power cycle is impossible.