Question

REALICE LOS SIGUIENTES PROBLEMAS DE ECUACIÓN DE LA RECTA CORRECTAMENTe

1.- Encuentre la ecuación vectorial de la recta si tenemos A(4, -2) y el vector V=(2, 5) paralelo a la recta y que pasa por A


2.- Encuentre la ecuación general de una recta conociendo un punto P(-2 ; 4) y su pendiente m= - 5 y grafique la recta.

Answer 1

1. La ecuación vectorial de la línea es
`\begin{bmatrix} & x & \\ & y & \end{bmatrix} =\begin{bmatrix} & 4 & \\ & -2 & \end{bmatrix} + t * \begin{bmatrix} & 2 & \\ & 5 & \end{bmatrix}`

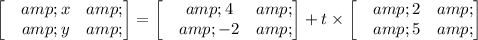
2. La ecuación de la recta es, y = -5·x - 6

Explanation:

1. El punto dado en la línea es A (4, -2), el vector paralelo a la línea es (2, 5)

Por tanto, la ecuación vectorial de la línea es;

`\begin{bmatrix} & x & \\ & y & \end{bmatrix} =\begin{bmatrix} & 4 & \\ & -2 & \end{bmatrix} + t * \begin{bmatrix} & 2 & \\ & 5 & \end{bmatrix}`

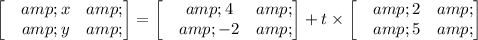
Donde;

t = Cualquier número

2. El punto por el que pasa la recta es P (-2; 4)

La pendiente de la recta, m = -5

Por lo tanto, la ecuación de la línea en forma de punto y pendiente se presenta de la siguiente manera;

y - 4 = (-5) · (x - (-2)) = -5 · x - 10

∴ y - 4 = -5 · x - 10 + 4 = -5 · x - 6

La ecuación de la recta es, y = -5·x - 6