Answer:
The number of hits would follow a binomial distribution with
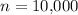 and
and
 .
.
The probability of finding
 hits is approximately
hits is approximately
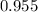 (or equivalently, approximately
(or equivalently, approximately
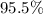 .)
.)
The mean of the number of hits is approximately
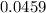 . The variance of the number of hits is approximately
. The variance of the number of hits is approximately
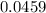 (not the same number as the mean.)
(not the same number as the mean.)
Step-by-step explanation:
There are
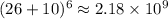 possible passwords in this set. (Approximately two billion possible passwords.)
possible passwords in this set. (Approximately two billion possible passwords.)
Each one of the
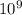 randomly-selected passwords would have an approximately
randomly-selected passwords would have an approximately
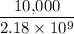 chance of matching one of the users' password.
chance of matching one of the users' password.
Denote that probability as
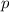 :
:
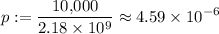 .
.
For any one of the
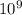 randomly-selected passwords, let
randomly-selected passwords, let
 denote a hit and
denote a hit and
 denote no hits. Using that notation, whether a selected password hits would follow a bernoulli distribution with
denote no hits. Using that notation, whether a selected password hits would follow a bernoulli distribution with
 as the likelihood of success.
as the likelihood of success.
Sum these
 's and
's and
 's over the set of the
's over the set of the
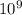 randomly-selected passwords, and the result would represent the total number of hits.
randomly-selected passwords, and the result would represent the total number of hits.
Assume that these
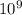 randomly-selected passwords are sampled independently with repetition. Whether each selected password hits would be independent from one another.
randomly-selected passwords are sampled independently with repetition. Whether each selected password hits would be independent from one another.
Hence, the total number of hits would follow a binomial distribution with
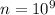 trials (a billion trials) and
trials (a billion trials) and
 as the chance of success on any given trial.
as the chance of success on any given trial.
The probability of getting no hit would be:
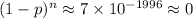 .
.
(Since
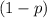 is between
is between
 and
and
 , the value of
, the value of
 would approach
would approach
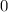 as the value of
as the value of
 approaches infinity.)
approaches infinity.)
The mean of this binomial distribution would be:
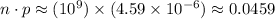 .
.
The variance of this binomial distribution would be:
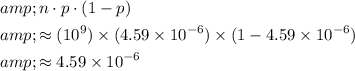 .
.