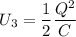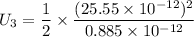The question is incomplete. The complete question is :
A dielectric-filled parallel-plate capacitor has plate area A = 10.0 cm2 , plate separation d = 10.0 mm and dielectric constant k = 3.00. The capacitor is connected to a battery that creates a constant voltage V = 15.0 V . Throughout the problem, use ϵ0 = 8.85×10−12 C2/N⋅m2 .
Find the energy U1 of the dielectric-filled capacitor. I got U1=2.99*10^-10 J which I know is correct. Now I need these:
1. The dielectric plate is now slowly pulled out of the capacitor, which remains connected to the battery. Find the energy U2 of the capacitor at the moment when the capacitor is half-filled with the dielectric.
2. The capacitor is now disconnected from the battery, and the dielectric plate is slowly removed the rest of the way out of the capacitor. Find the new energy of the capacitor, U3.
Solution :
Given :
d = 10 mm
= 0.010 m
Then, Capacitance,
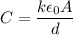
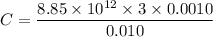
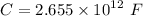
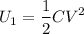
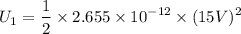
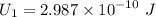
Now,
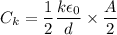
And
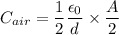
In parallel combination,
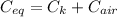
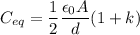
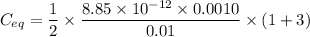
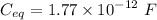
Then energy,

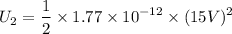
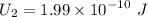
b). Now the charge on the
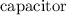 is :
is :
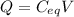


Now when the capacitor gets disconnected from battery and the
 is slowly
is slowly
 of the way out of the
of the way out of the
 is :
is :
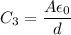
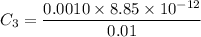

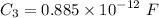
Without the dielectric,