Answer:
See explanation.
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Algebra I
Functions
- Exponential Property [Rewrite]:
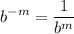
- Exponential Property [Root Rewrite]:
![\displaystyle \sqrt[n]{x} = x^{(1)/(n)}](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/pi5gzwebrzl682dhc5849e.png)
Calculus
Differentiation
- Derivatives
- Derivative Notation
Derivative Property [Multiplied Constant]:
![\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/sajvvpx1sytxjokl40ke2f.png)
Derivative Property [Addition/Subtraction]:
![\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/iqt7axoe8j2sh12ig7n0ah.png)
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Derivative Rule [Chain Rule]:
![\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/4e7e93dqa2auubmnlpfb3w.png)
Explanation:
We are given the following and are trying to find the second derivative at x = 2:
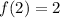
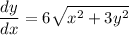
We can differentiate the 1st derivative to obtain the 2nd derivative. Let's start by rewriting the 1st derivative:
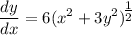
When we differentiate this, we must follow the Chain Rule:
![\displaystyle (d^2y)/(dx^2) = (d)/(dx) \Big[ 6(x^2 + 3y^2)^\big{(1)/(2)} \Big] \cdot (d)/(dx) \Big[ (x^2 + 3y^2) \Big]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/ufdwmpajdz9euwlp3zgpk4.png)
Use the Basic Power Rule:
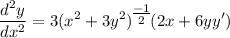
We know that y' is the notation for the 1st derivative. Substitute in the 1st derivative equation:
![\displaystyle (d^2y)/(dx^2) = 3(x^2 + 3y^2)^\big{(-1)/(2)} \big[ 2x + 6y(6√(x^2 + 3y^2)) \big]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/r40v4n2kgrvtr9owyb7cwa.png)
Simplifying it, we have:
![\displaystyle (d^2y)/(dx^2) = 3(x^2 + 3y^2)^\big{(-1)/(2)} \big[ 2x + 36y√(x^2 + 3y^2) \big]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/ty2cwolx8sq4op257i4dzj.png)
We can rewrite the 2nd derivative using exponential rules:
![\displaystyle (d^2y)/(dx^2) = (3\big[ 2x + 36y√(x^2 + 3y^2) \big])/(√(x^2 + 3y^2))](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/8pboie2zha9uncqo06aeyu.png)
To evaluate the 2nd derivative at x = 2, simply substitute in x = 2 and the value f(2) = 2 into it:
![\displaystyle (d^2y)/(dx^2) \bigg| \limits_(x = 2) = (3\big[ 2(2) + 36(2)√(2^2 + 3(2)^2) \big])/(√(2^2 + 3(2)^2))](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/vcqnexp37dys4klwcrc9ay.png)
When we evaluate this using order of operations, we should obtain our answer:
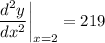
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Differentiation