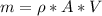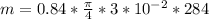Question

P9.28 A large vacuum tank, held at 60 kPa absolute, sucks sea- level standard air through a converging nozzle whose throat diameter is 3 cm. Estimate (a) the mass flow rate through the nozzle and (b) the Mach number at the throat.

Answer 1

a)
`m=0.17kg/s`

b)
`Ma=0.89`

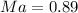
Step-by-step explanation:

From the question we are told that:

Pressure
`P=60kPa`

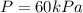
Diameter
`d=3cm`

Generally at sea level

`T_0=288k\\\\\rho_0=1.225kg/m^3\\\\P_0=101350Pa\\\\r=1.4`

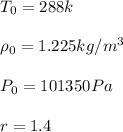
Generally the Power series equation for Mach number is mathematically given by

`(p_0)/(p)=(1+(r-1)/(2)Ma^2)^{(r)/(r-1)}`

`(101350)/(60*10^3)=(1+(1.4-1)/(2)Ma^2)^{(1.4)/(1.4-1)}`

`Ma=0.89`

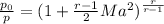
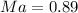
Therefore

Mass flow rate

`(\rho_0)/(\rho)=(1+(1.4-1)/(2)(0.89)^2)^{(1.4)/(1.4-1)}`

`(1.225)/(\rho)=(1+(1.4-1)/(2)(0.89)^2)^{(1.4)/(1.4-1)}`

`\rho=0.848kg/m^3`

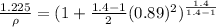
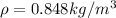
Generally the equation for Velocity at throat is mathematically given by

`V=Ma(r*T_0√(T_e)`)

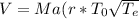Where

`T_e=(P_e)/(R\rho)\\\\T_e=(60*10^6)/(288*0.842\rho)`

`T_e=248`

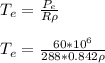
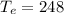
Therefore

`V=0.89(1.4*288√(248))\\\\V=284`

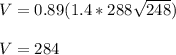
Generally the equation for Mass flow rate is mathematically given by

`m=\rho*A*V`

`m=0.84*(\pi)/(4)*3*10^(-2)*284`

`m=0.17kg/s`