Question

Factoring quadratic trinomials.

List down all the factors of (13).
List down the sum of (40).
Identify which two factors add up to 13.
x^2 + 13x + 40
​

Answer 1

The correct solution is "x = -5 and x = -8".

Explanation:

The given equation is:

⇒
`x^2+13x+40=0`

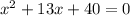
On factorizing the above equation, we get

⇒
`x^2+5x+8x+40=0`

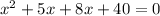
On taking "x" common, we get

⇒
`x(x+5)+8(x+5)=0`

⇒
`(x+5)(x+8)=0`

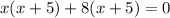
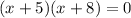
Now,

⇒
`x+5=0`

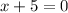
On subtracting "5" from both sides, we get

⇒
`x+5-5=0-5`

⇒
`x=-5`

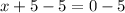
Or,

⇒
`x+8=0`

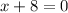
On subtracting "8" from both sides, we get

⇒
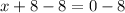
`x+8-8=0-8`

⇒
`x=-8`