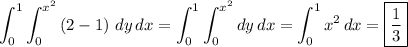Question

Use green's theorem to find integral subscript c left parenthesis y space plus space e to the power of square root of x end exponent right parenthesis d x space plus space left parenthesis 2 x plus cos open parentheses y squared close parentheses right parenthesis d y, where c is the boundary of the region bounded by the parabola y = x2 and the lines y = 0 and x = 1. A right parenthesis space e plus cos left parenthesis 1 right parenthesis b right parenthesis space e minus cos left parenthesis 2 right parenthesis c right parenthesis space e to the power of 1 divided by 2 end exponent minus cos left parenthesis 4 right parenthesis d right parenthesis space e to the power of 1 divided by 2 end exponent plus cos left parenthesis 1 right parenthesis e right parenthesis space 1 third.

Answer 1

My best interpretation of the math here is that you're talking about the line integral,

`\displaystyle \int_C \left(y+e^(\sqrt x)\right) \, dx + \left(2x + \cos\left(y^2\right)\right) \, dy`

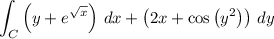
I won't bother trying to decipher what look like multiple choice solutions.

By Green's theorem, the line integral above is equivalent to

`\displaystyle \iint_D (\partial\left(2x+\cos\left(y^2\right)\right))/(\partial x) - (\partial\left(y+e^(\sqrt x)\right))/(\partial y) \, dx \, dy`

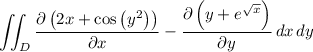
where D is the set

`D = \left\{ (x, y) : 0 \le x \le 1 \text{ and } 0 \le y \le x^2 \right\}`

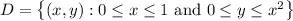
Compute the double integral:

`\displaystyle \int_0^1 \int_0^(x^2) \left(2 - 1\right) \, dy \, dx = \int_0^1 \int_0^(x^2) dy \, dx = \int_0^1 x^2 \, dx = \boxed{\frac13}`