Explanation:
The equation will form a circle because it in the form of
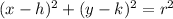
First, let set the equation equal.
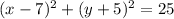
Here the center will be (7,-5), and the radius of 5. The boundary line will be dashed
Since this is in the inequalities, we must find the solution set.
Plug in 0,0 for x and y and see if it's true.
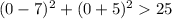
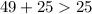
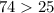
This is a true so we shade the region that includes 0,0
Since 0,0 has a greater distance from the center of the circle, 0,0 is outside of the circle, so our solution set will
be outside of circle.
Here a picture of graph,