Question

Please,look at this one.

Answer 1

9514 1404 393

Answer:

x = √2

Explanation:

A graph indicates the only solution is near x=√2.

__

Square both sides, separate the radical and do it again.

`\displaystyle(2-x)\sqrt{(x+2)/(x-1)}=√(x)+√(3x-4)\qquad\text{given}\\\\(2-x)^2\cdot(x+2)/(x-1)=x+(3x-4)+2√(x(3x-4))\qquad\text{square}\\\\((2-x)^2(x+2))/(x-1)-4x+4=2√(x(3x-4))\qquad\text{isolate radical}\\\\\left(((2-x)^2(x+2)-4(x-1)^2)/(x-1)\right)^2=x(3x-4)\qquad\text{square}\\\\(x^3-6x^2+4x+4)^2=4(x-1)^2(3x^2-4x)\qquad\text{multiply by $(x-1)^2$}`

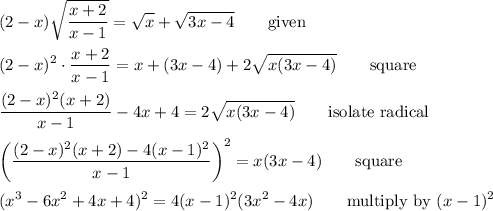
Now, we can put this polynomial equation into standard form and factor it.

`x^6 -12x^5+32x^4-76x^2+48x+16=0\\\\(x-2)^2(x^2-2)(x^2-8x-2)=0\qquad\text{factor it}\\\\x\in \{2,\pm√(2),4\pm3√(2)\}`

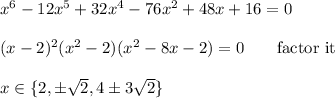
The original equation requires that we restrict the domain of possible solutions. In order for the radicals to be non-negative, we must have x ≥ 4/3. In order for the left side of the equation to be non-negative, we must have x ≤ 2. So, the only potential solutions will be in the interval [4/3, 2].

The only values in the above list that match this requirement are {√2, 2}. We know that the right side of the equation cannot be zero, so the value x=2 is also an extraneous solution.

The only solution is x = √2.

_____

Additional comment

For solving higher-degree polynomials, I like to use a graphing calculator to help me find the roots. The second attachment shows the roots of the 6th-degree polynomial. They can help us factor the equation. (There are also various machine solvers available that will show factors and roots.)