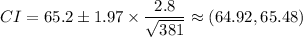Question

A survey of 381 adult females produced a mean height of 65.2 inches with a standard deviation of 2.8 inches. Construct a confidence interval based on a 95% confidence level.

(64.83, 65.57)
(65.19, 65.21)
(64.96, 65.44)
(64.92, 65.48)

Answer 1

(64.92, 65.48)

Explanation:

The given details are;

The number of adults in the survey, n = 381 adults

The mean height of the adults in the survey,
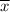`\overline x` = 65.2 inches

The standard deviation of the height of the adults in the survey, s = 2.8 inches

The confidence interval is given as follows;

`CI=\bar{x}\pm t_(\alpha /2) \cdot (s)/(√(n))`

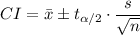
The test statistic for a 95% confidence interval with α = 0.05, the degrees of freedom, df = n-1 = 381 - 1 = 380,
`t_(\alpha /2, df)` =
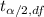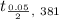`t_{(0.05)/(2) , \ 381}` = 1.97

Therefore, we get;

C.I =

`CI=65.2\pm 1.97 * (2.8)/(√(381)) \approx (64.92, 65.48)`