Question

HELP

Rehan proved by mathematical induction that for all
the positive integers, n°
+ 2n is divisible by 3. Can
you find an integer counterexample to show that
this statement is not true? Explain.

Answer 1

If your teacher wants you to find a positive integer for n that will make
`n^3+2n` not divisible by 3, then you'll be searching for quite a while.

This is because Rehan is correct in the statement that
`n^3+2n` is divisible by 3 for any positive integer n.

n = {1,2,3,...}

For example, if n = 5, then

`n^3+2n = 5^3+2(5) = 125+10 = 135`

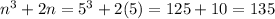
That is divisible by 3 because 135/3 = 45 is a whole number result without any decimal or fractional extras.

---------------

Here's the proof that Rehan probably used or set up.

Base case: Plug in n = 1 to find that
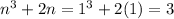`n^3+2n = 1^3+2(1) = 3` which is definitely divisible by 3.

Inductive step:

Assume that
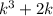`k^3+2k` is divisible by 3 for some integer k > 1.

The goal is to then show it leads to
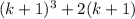`(k+1)^3+2(k+1)` is also divisible by 3.

Skipping a bunch of steps, you should find that
`(k+1)^3+2(k+1) = (k^3+2k) + 3(k^2+k+1)`

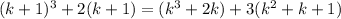
The first part k^3+2k is already assumed to be a multiple of 3, so we don't need to worry about it. The second part 3(k^2+k+1) is also a multiple of 3 because 3 is a factor.

Summing any two multiples of 3 gets us another multiple of 3.

Therefore, this concludes the proof that Rehan would have done. There are probably alternative proof methods he could have used, but he likely followed these steps or similar when doing the induction proof.

---------------

Long story short, the fact that the statement
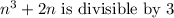`n^3+2n \text{ is divisible by } 3` is proven to work with any integer n from the set {1,2,3,...} means that we cannot find a counterexample.