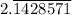Question

The graph of the continuous function f consists of three line segments, as shown in the figure above. What is the average value of f on the interval [−1,6] ?

Answer 1

The average value of the function on the interval [-1, 6] is
`2.\overline{1428571}`

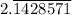
Step-by-step explanation:

The given

The average of a function is the height, 'h', of a rectangle with a width equivalent to the given interval and an area equivalent to the area of the function

The area under the graph of the function between the interval [-1, 6] consist of two right triangles and a rectangle and it is therefore given as follows;

The area. A = 1/2 × (0 - (-1)) × 2 + 2 × (6 - 0) + 1/2 × (4 - 2) × (6 - 4) = 15

The width of the rectangle, w = (6 - (-1)) = 7

w = 7

The area of the rectangle = h × w = A = 15

∴ The average value of the function, f = h = A/w = 15/7 =
`2.\overline{1428571}`