Question

In a circle with radius 2.1, an angle intercepts an arc of length 21.2. Find the angle in

radians to the nearest 10th.

Answer 1

Given:

Radius of a circle = 2.1 units

Arc length = 21.2 units

To find:

The central angle in radians to the nearest 10th.

Solution:

We know that the intercepted arc length is

`s=r\theta`

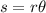
Where, s is the arc length, r is the radius and
`\theta` is the central angle in radians.

Putting the given values, we get

`21.2=2.1\theta`

`(21.2)/(2.1)=\theta`

`10.095238=\theta`

`\theta\approx 10.1`

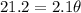
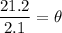
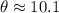
Therefore, the angle in radians is 10.1.