Final Answer:
The reaction is approximately 2.081 times faster at 322 K than at 310 K.
Step-by-step explanation:
To determine how much faster a reaction is at one temperature versus another, we can use the Arrhenius equation, which is given by:
![\[ k = Ae^{-(E_a)/(RT)} \]](https://img.qammunity.org/2022/formulas/chemistry/college/c2fznm7d4njo497tzk34hlsmboyed33ky5.png)
where:
- k is the rate constant of the reaction
- A is the pre-exponential factor, which is a constant for a given reaction
- E_a is the activation energy
- R is the gas constant
- T is the temperature in Kelvin
To find out how much faster the reaction is at 322 K compared to 310 K, we need to find the rate constants at these temperatures (
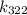 and
and
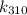 ), and then take their ratio. We won't need the value of A because we are interested in the ratio of rate constants, and A will cancel out.
), and then take their ratio. We won't need the value of A because we are interested in the ratio of rate constants, and A will cancel out.
Let's calculate
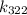 and
and
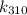 using the activation energy
using the activation energy
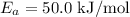 and
and
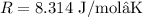 . Remember to convert the activation energy to the same units as R, which are J/mol.
. Remember to convert the activation energy to the same units as R, which are J/mol.
First, convert E_a to J/mol:
![\[ E_a = 50.0 \text{ kJ/mol} * 1000 \text{ J/kJ} = 50000 \text{ J/mol} \]](https://img.qammunity.org/2022/formulas/chemistry/college/vvw14sq955fj9sescw3r2x8bfdxhiyu1ry.png)
Now, calculate k_{322}:
![\[ k_(322) = Ae^{-\frac{50000 \text{ J/mol}}{(8.314 \text{ J/mol•K})(322 \text{ K})}} \]](https://img.qammunity.org/2022/formulas/chemistry/college/nm6pb1wrwlgrtk3i796uijvjpql5e3v9be.png)
Simplifying inside the exponent:
![\[ -(50000)/((8.314)(322)) \approx -18.691 \]](https://img.qammunity.org/2022/formulas/chemistry/college/ae5wdu95cp7h0gfk7gmzveaj1ik6wx4qrw.png)
Now,
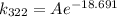
Next, calculate
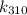 :
:
![\[ k_(310) = Ae^{-\frac{50000 \text{ J/mol}}{(8.314 \text{ J/mol•K})(310 \text{ K})}} \]](https://img.qammunity.org/2022/formulas/chemistry/college/ya270okws9lp3mda2opbm7jqk80udz78hj.png)
Simplifying inside the exponent:
![\[ -(50000)/((8.314)(310)) \approx -19.424 \]](https://img.qammunity.org/2022/formulas/chemistry/college/p5sicx5wt7872o745d6u6guhr2bpckuq0f.png)
So,
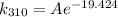
To find out how much faster the reaction is at 322 K than at 310 K, we take the ratio of
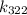 over
over
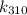 :
:
![\[ (k_(322))/(k_(310)) = (Ae^(-18.691))/(Ae^(-19.424)) \]](https://img.qammunity.org/2022/formulas/chemistry/college/j8ki1pq44z8s4joifh7vn4gqtm4gu9rmo6.png)
Because A is the same for both rate constants and we are only interested in the ratio, it cancels out:
![\[ (k_(322))/(k_(310)) = (e^(-18.691))/(e^(-19.424)) \]](https://img.qammunity.org/2022/formulas/chemistry/college/i7c85xicgmhtmhtml6ih147yyoytihf4b3.png)
Using properties of exponents, we can combine the exponents:
![\[ (k_(322))/(k_(310)) = e^((-18.691) - (-19.424)) = e^(19.424 - 18.691) = e^(0.733) \]](https://img.qammunity.org/2022/formulas/chemistry/college/vm4vlgyfhwgea926egfgyotzfnxn6wvl3g.png)
Using a calculator to find the value of
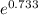 :
:
![\[ (k_(322))/(k_(310)) \approx e^(0.733) \approx 2.081 \]](https://img.qammunity.org/2022/formulas/chemistry/college/m4bqkic9q8fcceq9lgvh1lldum0as7kt5s.png)
This result means that the reaction is approximately 2.081 times faster at 322 K than at 310 K.