Answer:
The standard deviation of the data set is
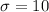
Explanation:
The formula for standard deviation is
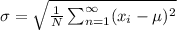 where you are basically taking the mean of the data set (
where you are basically taking the mean of the data set (
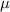 ), find the mean of the squared differences from the observed values and mean (
), find the mean of the squared differences from the observed values and mean (
 ), and square root the result:
), and square root the result:
Mean:
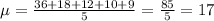
Average of squared differences (variance):
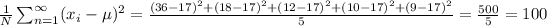
Standard deviation:
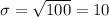
This means that the standard deviation of the data set is 10, which tells us that the values of the data set, on average, are separated by 10.