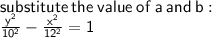Question

Hey Mahfia, please help! Find an equation in standard form for the hyperbola with vertices at (0, ±10) and asymptotes at

y = ±
`(5)/(6) x`

Answer 1

`\huge\boxed{ \red{ \boxed{ \tt{ \frac{ {y}^(2) }{ {10}^(2) } - \frac{ {x}^(2) }{ {12}^(2) } = 1}}}}`

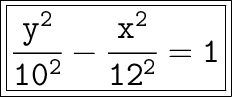
Explanation:

to understand this

you need to know about:

• conic sections
• PEMDAS

tips and formulas:

• 
  `\sf hyperbola \:equation : \\ \sf \frac{ {x}^(2) }{ {a}^(2) } - \frac{ {y}^(2) }{ {b}^(2) } = 1`
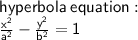
• vertices of hyperbola:(±a,0) and (0,±b) if reversed
• 
  `\sf \: asymptotes : \\ y = \pm(b)/(a) x`

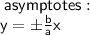
given:

• vertices: (0,±10)
• the hyperbola equation is inversed since the vertices is (0,±10)
• asymptotes:
  `\pm (5)/(6)x`

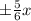
let's solve:

• the asymptotes are in simplest and we know b is ±10

according to the question

1. 
   `y = \sf (5 * 2)/(6 * 2) x \\ y = (10)/(12) x`

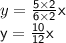
therefore we got

• a=12
• b=10

note: the equation will be inversed

let's create the equation:

1. 
   `\sf substitute \: the \: value \: of \: a \: and \: b : \\ \sf \frac{ {y}^(2) }{ {10}^(2) } - \frac{ {x}^(2) }{ {12}^(2) } = 1`