Question

Solve using the Pythagorean identity
​

Answer 1

`\bold{Sin\theta_(1)=-(4)/(5)}`

Answer:

Solution given

Cos
`\displaystyle \theta_(1)=(3)/(5)`

consider Pythagorean theorem

`\bold{Sin²\theta+Cos²\theta=1}`

Subtracting
`Cos²\theta`both side

`\displaystyle Sin²\theta=1-Cos²\theta`

doing square root on both side we get

`Sin\theta=√(1-Cos²\theta)`

Similarly

`Sin\theta_(1)=\sqrt{1-Cos²\theta_(1)}`

Substituting value of
`Cos\theta_(1)`

we get

`Sin\theta_(1)=\sqrt{1-((3)/(5))²}`

Solving numerical

`Sin\theta_(1)=\sqrt{1-((9)/(25))}`

`Sin\theta_(1)=\sqrt{(16)/(225)}`

`Sin\theta_(1)=(√(2*2*2*2))/(√(5*5))`

`Sin\theta_(1)=(4)/(5)`

Since

In IVquadrant sin angle is negative

`\bold{Sin\theta_(1)=-(4)/(5)}`

Answer 2

`\sin(\theta_1)=-(4)/(5)`

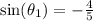
Explanation:

We'll use the Pythagorean Identity
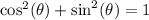`\cos^2(\theta)+\sin^2(\theta)=1` to solve this problem.

Subtract
`\cos^2(\theta)` from both sides to isolate
`\sin^2(\theta)`:

`\sin^2(\theta)=1-\cos^2(\theta)`

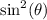Substitute
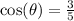`\cos(\theta)=(3)/(5)` as given in the problem:

`\sin^2(\theta_1)=1-((3)/(5)^2)`

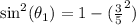
Simplify:

`\sin^2\theta_1=1-(9)/(25)`

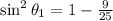
Combine like terms:

`\sin^2\theta_1=(16)/(25)`

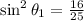
For
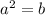`a^2=b`, we have two solutions
`a=\pm √(b)`:

`\sin\theta_1=\pm \sqrt{(16)/(25)},\\\begin{cases}\sin \theta_1=(4)/(5),\\\sin \theta_1=\boxed{-(4)/(5)}\end{cases}`

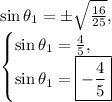
Since the sine of all angles in quadrant four return a negative output,
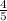`(4)/(5)` is extraneous and our answer is
`\boxed{\sin(\theta_1)=-(4)/(5)}`