Answer:

General Formulas and Concepts:
Calculus
Explanation:
Step 1: Define
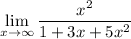
Step 2: Determine Rule
If the highest power of x in a rational expression is the same both numerator and denominator, then the limit as x approached ∞ would be the highest term coefficient in the numerator divided by the highest term coefficient in the denominator.
Step 3: Identify
Numerator highest power: x²
Denominator highest power: 5x²
Step 4: Evaluate
Apply rule.

Topic: AP Calculus AB/BC (Calculus I/II)
Unit: Limits
Book: College Calculus 10e