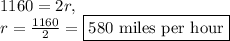Question

A small airplane flies 1160 miles with an average speed of 290 miles per hour. 2 hours after the plane leaves, a Boeing 747 leaves from the same point. Both planes arrive at the same time; what was the average speed of the 747 ?

Answer 1

`580\text{ miles per hour}`

Explanation:

To solve this problem, we can use the formula
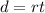`d=rt`, where
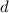`d` is distance,
`r` is rate, and
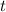`t` is time.

Let's start by calculating how long the small airplane takes to complete the journey. The distance is 1160 miles and the rate is 290 miles per hour. Therefore, we have:

`1160=290t,\\t=(1160)/(290)=4\text{ hours}`

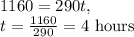
Since the Boeing 747 left 2 hours after the small airplane left, the small airplane has just
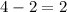`4-2=2` hours left of travelling time.

Therefore, to arrive at the same time as the small airplane, the Boeing 747 must cover the same distance of 1160 miles in only 2 hours. Hence, the Boeing 747's speed must have been:

`1160=2r,\\r=(1160)/(2)=\boxed{580\text{ miles per hour}}`