Answer:
9 mph = the speed in still water
Explanation:
Let r = the speed in still water
Then the speed going down stream is r + 3
and the speed going upstream is r - 3
d = rt or t = d/r
time going downstream is 16/(r + 3) and time going upstream is 16/(r - 3)
The total time was 4 hours, so
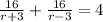 Multiply thru the equation by (r + 3)(r - 3)
Multiply thru the equation by (r + 3)(r - 3)
Then 16(r - 3) + 16(r + 3) = 4(r + 3)(r - 3)
16r - 48 + 16r + 48 =
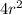 - 36
- 36
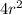 - 36 = 32r
- 36 = 32r
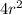 - 32r - 36 = 0
- 32r - 36 = 0

4(r - 9)(r + 1) = 0
r = 9 or -1
But a rate of speed cannot be negative, so x ≠ -1
So, r = 9 mph = the speed in still water