Question

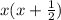
Write each expression as a product of linear factors 1. X^2+1/2x 2. X^2+2x-3 3. (2x-3)^2 4. X^3+2x^2-19x-20

Answer 1

1. X^2+1/2x =
`x(x+(1)/(2))`

2. X^2+2x-3 =
`(x-1)(x+3)`

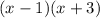
3. (2x-3)^2 = (2x-3)(2x-3)

4. X^3+2x^2-19x-20 =
`(x+1)(x-4)(x+5)`

Explanation:

Each expression can be written as a product of linear factors as follows

1. X^2+1/2x ⇒
`x^(2) + (1)/(2)x`

`x^(2) + (1)/(2)x` =
`x(x+(1)/(2))`

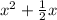
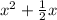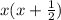
Hence, X^2+1/2x =
`x(x+(1)/(2))`

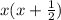
2. X^2+2x-3 ⇒
`x^(2) +2x-3`

`x^(2) +2x-3 = x^(2) +3x-x-3`

`x^(2) +3x-x-3 = x(x+3) -1(x+3)`

`x(x+3) -1(x+3) = (x-1)(x+3)`

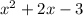
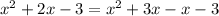
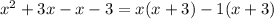
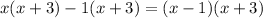
Hence, X^2+2x-3 =
`(x-1)(x+3)`

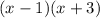
3. (2x-3)^2 ⇒
`(2x-3)^(2)`

`(2x-3)^(2) = (2x-3)(2x-3)`

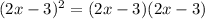
Hence, (2x-3)^2 = (2x-3)(2x-3)

4. X^3+2x^2-19x-20 ⇒
`x^(3)+2x^(2) -19x -20`

`x^(3)+2x^(2) -19x -20 = (x+1)(x^(2) +x-20)`

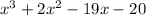
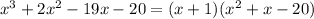
First,

`x^(2) +x-20 = x^(2) +5x-4x-20\\x^(2) +5x-4x-20= x(x+5)-4(x+5)\\x(x+5)-4(x+5) = (x-4)(x+5)`

∴
`(x+1)(x^(2) +x-20) = (x+1)(x-4)(x+5)`

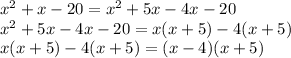
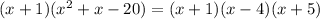
Hence, X^3+2x^2-19x-20 =
`(x+1)(x-4)(x+5)`