Answer:
There are two possible solutions for the other two vertices of the rectangle:
(i) (4, 1), (-1, 1), (ii) (4, -7), (-1, -7)
Explanation:
Geometrically speaking, the perimeter of a rectangle (
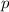 ) is:
) is:
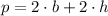 (1)
(1)
Where:
 - Base of the rectangle.
- Base of the rectangle.
 - Height of the rectangle.
- Height of the rectangle.
Let suppose that the base of the rectangle is the line segment between (4, -3) and (-1, -3). The length of the base is calculated by Pythagorean Theorem:
![b = \sqrt{[(-1)-4]^(2)+[(-3)-(-3)]^(2)}](https://img.qammunity.org/2022/formulas/mathematics/high-school/naqn0epnr5952ok2wrsbaq6vott3sm4i93.png)
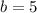
If we know that
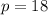 and
and
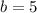 , then the height of the rectangle is:
, then the height of the rectangle is:

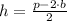
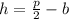
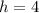
There are two possible solutions for the other two vertices of the rectangle:
(i) (4, 1), (-1, 1), (ii) (4, -7), (-1, -7)