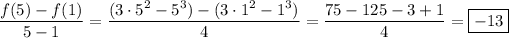The average rate of change of a function f(x) over some interval [a, b] is the difference quotient,
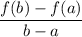
which corresponds to the slope of the line connecting the points (a, f(a)) and (b, f(b)) in the graph of f(x).
Given f(x) = 3x² - x³ (correct me if I'm wrong, the exponents look cut off in your screenshot), the average rate of change on [1, 5] is