Answer:
B) 4√2
General Formulas and Concepts:
Calculus
Differentiation
- Derivatives
- Derivative Notation
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Parametric Differentiation
Integration
- Integrals
- Definite Integrals
- Integration Constant C
Arc Length Formula [Parametric]:
![\displaystyle AL = \int\limits^b_a {√([x'(t)]^2 + [y(t)]^2)} \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/uvh5be2ih4rw251okyu2k2bn4otxq4jxzf.png)
Explanation:
Step 1: Define
Identify
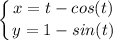
Interval [0, π]
Step 2: Find Arc Length
- [Parametrics] Differentiate [Basic Power Rule, Trig Differentiation]:
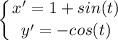
- Substitute in variables [Arc Length Formula - Parametric]:
![\displaystyle AL = \int\limits^(\pi)_0 {√([1 + sin(t)]^2 + [-cos(t)]^2)} \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/7r2bfw4pfd9s20neyykblqx9on499a4yr1.png)
- [Integrand] Simplify:
![\displaystyle AL = \int\limits^(\pi)_0 {√(2[sin(x) + 1]) \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/9umoqudeeoa1lo46zj4q1la3kmabw11opw.png)
- [Integral] Evaluate:
![\displaystyle AL = \int\limits^(\pi)_0 {√(2[sin(x) + 1]) \, dx = 4√(2)](https://img.qammunity.org/2022/formulas/mathematics/high-school/ojzq7uja92f1w9d7xwnne2ypuclc3egcva.png)
Topic: AP Calculus BC (Calculus I + II)
Unit: Parametric Integration
Book: College Calculus 10e