Question

a pair of fair dice is rolled anf the sum of the numbers is noted. determine the probability that one die resulted in a 3, given that the sum is 8. g

Answer 1

0.4 = 40% probability that one die resulted in a 3.

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

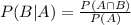
In which

P(B|A) is the probability of event B happening, given that A happened.

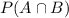`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

Outcomes for the dice:

For the pair of dice:

(1,1), (1,2), (1,3), (1,4), (1,5), (1,6)

(2,1), (2,2), (2,3), (2,4), (2,5), (2,6)

(3,1), (3,2), (3,3), (3,4), (3,5), (3,6)

(4,1), (4,2), (4,3), (4,4), (4,5), (4,6)

(5,1), (5,2), (5,3), (5,4), (5,5), (5,6)

(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)

So 36 total outcomes.

In this question:

Event A: Sum of 8

Event B: One dice resulting in 3.

Probability of a sum of 8:

These are the following desired outcomes:

(2,6), (3,5), (4,4), (5,3), (6,2)

5 outcomes out of 36, so:

`P(A) = (5)/(36)`

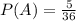
Probability of a sum of 8 and one dice resulting in 3.

(3,5) or (5,3), so 2 outcomes out of 36, and:

`P(A \cap B) = (2)/(36)`

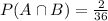
Probability that one die resulted in a 3, given that the sum is 8:

`P(B|A) = (P(A \cap B))/(P(A)) = ((2)/(36))/((5)/(36)) = (2)/(5) = 0.4`

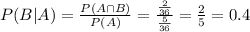
0.4 = 40% probability that one die resulted in a 3.