Question

There are 11 students on a committee. To decide which 4 of these students will attend a conference, 4 names are chosen at random by pulling names one at a time from a hat. What is the probability that Sarah, Jamal, Kate, and Mai are chosen in any order

Answer 1

The probability of choosing Sarah, Jamal, Kate, and Mai from a committee of 11 students for 4 conference spots is calculated using the hypergeometric distribution and is approximately 0.00303.

Step-by-step explanation:

The question involves calculating the probability of selecting 4 specific individuals from a group. This scenario can be modeled using the hypergeometric distribution, as we are selecting without replacement from two distinct groups (those who are picked to attend the conference and those who are not).

There are 11 people in total and 4 spots available; the probability of choosing Sarah, Jamal, Kate, and Mai in any order is found by dividing the number of successful outcomes (1, since there is only one way to choose all four specific individuals) by the total number of ways to choose any 4 out of 11 students.

To calculate the total number of ways to choose 4 out of 11 students, we use the combination formula, which is C(n, k) = n! / (k! * (n-k)!), where 'n' is the total number of items, 'k' is the number of items to choose, and '!' denotes factorial. For this case, n=11 and k=4. The calculation is as follows:

C(11, 4) = 11! / (4! * (11-4)!) = 330

Thus, the probability P that Sarah, Jamal, Kate, and Mai are chosen is:

P = 1 / C(11, 4) = 1 / 330 ≈ 0.00303

Answer 2

0.003 = 0.3% probability that Sarah, Jamal, Kate, and Mai are chosen in any order.

Step-by-step explanation:

The students are chosen without replacement, which means that the hypergeometric distribution is used to solve this question.

Hypergeometric distribution:

The probability of x successes is given by the following formula:

`P(X = x) = h(x,N,n,k) = (C_(k,x)*C_(N-k,n-x))/(C_(N,n))`

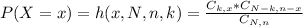
In which:

x is the number of successes.

N is the size of the population.

n is the size of the sample.

k is the total number of desired outcomes.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

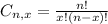
In this question:

11 students means that
`N = 11`

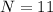
4 are Sarah, Jamal, Kate, and Mai, so
`k = 4`

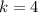
4 are chosen, which means that
`n = 4`

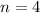
What is the probability that Sarah, Jamal, Kate, and Mai are chosen in any order?

This is P(X = 4). So

`P(X = x) = h(x,N,n,k) = (C_(k,x)*C_(N-k,n-x))/(C_(N,n))`

`P(X = 4) = h(4,11,4,4) = (C_(4,4)*C_(7,0))/(C_(11,4)) = 0.003`

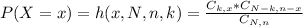
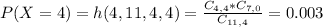
0.003 = 0.3% probability that Sarah, Jamal, Kate, and Mai are chosen in any order.