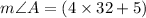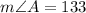Question

Quadrilateral ABCD is inscribed In a circle.
What is the measure of angle A?

Answer 1

`m\angle A = 133\degree`

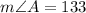
Explanation:

Quadrilateral ABCD is inscribed In a circle.

So, ABCD is a cyclic Quadrilateral.

Opposite angles of a cyclic quadrilateral are supplementary.

Therefore,

(4x + 5)° + (x + 15)° = 180°

(4x + 5 + x + 15)° = 180°

(5x + 20)° = 180°

5x + 20 = 180

5x = 180 - 20

5x = 160

x = 160/5

x = 32

`m\angle A = (4x + 5)\degree`

`m\angle A = (4* 32+ 5)\degree`

`m\angle A = (128+ 5)\degree`

`m\angle A = 133\degree`