Question

A soap bubble, when illuminated at normal incidence with light of 463 nm, appears to be especially reflective. If the index of refraction of the film is 1.35, what is the minimum thickness the soap film can be if it is surrounded by air

Answer 1

the minimum thickness the soap film can be if it is surrounded by air is 85.74 nm

Step-by-step explanation:

Given the data in the question;

wavelength of light; λ = 463 nm = 463 × 10⁻⁹ m

Index of refraction; n = 1.35

Now, the thinnest thickness of the soap film can be determined from the following expression;

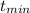`t_{min` = ( λ / 4n )

so we simply substitute in our given values;

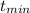`t_{min` = ( 463 × 10⁻⁹ m ) / 4(1.35)

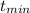`t_{min` = ( 463 × 10⁻⁹ m ) / 5.4

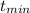`t_{min` = ( 463 × 10⁻⁹ m ) / 4(1.35)

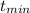`t_{min` = 8.574 × 10⁻⁸ m

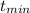`t_{min` = 85.74 × 10⁻⁹ m

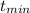`t_{min` = 85.74 nm

Therefore, the minimum thickness the soap film can be if it is surrounded by air is 85.74 nm