Question

Insurance companies are interested in knowing the population percent of drivers who always buckle up before riding in a car. They randomly survey 401 drivers and find that 294 claim to always buckle up. Construct a 90% confidence interval for the population proportion that claim to always buckle up. Use interval notation, for example, [1,5].

Answer 1

[0.6969, 0.7695]

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
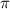`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

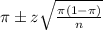
In which

z is the z-score that has a p-value of
`1 - (\alpha)/(2)`.

They randomly survey 401 drivers and find that 294 claim to always buckle up.

This means that
`n = 401, \pi = (294)/(401) = 0.7332.<strong> </strong></p><p><strong>90% confidence level </strong></p><p>So [tex]\alpha = 0.1`, z is the value of Z that has a p-value of
`1 - (0.1)/(2) = 0.95`, so
`Z = 1.645`.

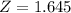The lower limit of this interval is:

`\pi - z\sqrt{(\pi(1-\pi))/(n)} = 0.7332 - 1.645\sqrt{(0.7332*0.2668)/(401)} = 0.6969`

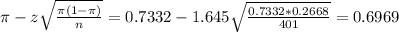
The upper limit of this interval is:

`\pi + z\sqrt{(\pi(1-\pi))/(n)} = 0.7332 + 1.645\sqrt{(0.7332*0.2668)/(401)} = 0.7695`

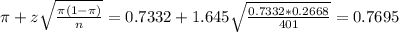
The 90% confidence interval for the population proportion that claim to always buckle up is [0.6969, 0.7695]