Answer:
[0.6969, 0.7695]
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
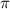 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.
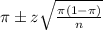
In which
z is the z-score that has a p-value of
 .
.
They randomly survey 401 drivers and find that 294 claim to always buckle up.
This means that
![n = 401, \pi = (294)/(401) = 0.7332.<strong> </strong></p><p><strong>90% confidence level </strong></p><p>So [tex]\alpha = 0.1](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/swzuiedjygmive3ws224c4.png) , z is the value of Z that has a p-value of
, z is the value of Z that has a p-value of
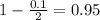 , so
, so
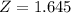 .
.
The lower limit of this interval is:
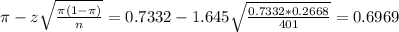
The upper limit of this interval is:
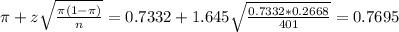
The 90% confidence interval for the population proportion that claim to always buckle up is [0.6969, 0.7695]