Question

CAN SOMEONE PLEASE ANSWER THE FOLLOWING IT URGENT

Answer 1

See bolded below.

Explanation:

As you said, you only need help with no. 2:

a) Check the attachments for the lines

b) The equations are, respectively:

y = -4x + 1 [intersects parabola at 1 point]

Check:

`\begin{bmatrix}y=\left(x-2\right)^2-3\\ y=-4x+1\end{bmatrix}`

`\begin{bmatrix}-4x+1=\left(x-2\right)^2-3\end{bmatrix}`

`\begin{bmatrix}-4x+1=x^2-4x+1\end{bmatrix}`

`x^2=0, x = 0`

`y=-4\cdot \:0+1 = 1`

`y=1,\:x=0`

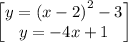
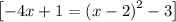
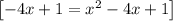
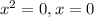
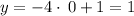
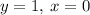
The point of intersection would be (0, 1)

y = -4x + 3 [intersects parabola at 2 points]

Check:

`\begin{bmatrix}y=\left(x-2\right)^2-3\\ y=-4x+3\end{bmatrix}`

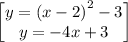
Subtract the 2 equations,

`y=\left(x-2\right)^2-3\\-\\\underline{y=-4x+3}\\y-y=\left(x-2\right)^2-3-\left(-4x+3\right),\\0=x^2-2\\x = √(2), x = - √(2) \\\\\mathrm{Plug\:the\:solutions\:}x=√(2),\:x=-√(2)\mathrm{\:into\:}y=\left(x-2\right)^2-3`

`\begin{pmatrix}x=√(2),\:&y=3-4√(2)\\ x=-√(2),\:&y=3+4√(2)\end{pmatrix}`

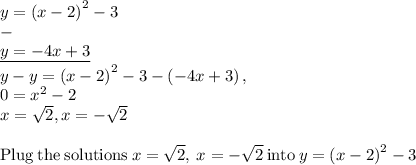
Therefore the points of intersection are (√2, 3-4√2) and (-√2, 3+4√2) respectively

And finally we have the equation y = - 4x. It doesn't intersect the parabola.

c) The y-intercepts of such graphs are all less than or equal to 0.