Answer:
The midsegment is 58 units long.
Explanation:
Midsegment Theorem:
It states that the length of the midsegment is half the length of the parallel side.
In this question:
Midsegment: 2x + 8
Parallel side: 5x - 9
Parallel side is double the midsegment. So, we use this to find x:
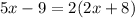
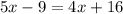
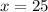
Midsegment:
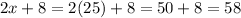
The midsegment is 58 units long.