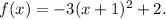Question

WILL MARK!!

Select the correct answer.
Which function does this graph represent?

Answer 1

I believe the answer is C

Explanation:

Answer 2

the correct answer which function does this graph represent is: B

The given quadratic functions, let's consider the general form of a quadratic function:

`\[f(x) = ax^2 + bx + c\]`

In this case, the functions are already in the form:

`A. \(f(x) = 3(x+1)^2 + 2\)`

`B. \(f(x) = -3(x+1)^2 + 2\)`

`C. \(f(x) = -3(x+1)^2 - 2\)`

`D. \(f(x) = 3(x-1)^2 + 2\)`

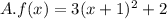
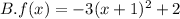
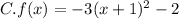
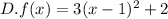
Let's compare them to the standard form
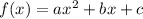`\(f(x) = ax^2 + bx + c` to identify the values of
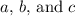`\(a\), \(b\), and \(c\)` in each case:

`A. \(a = 3\), \(b = 6\), \(c = 2\)`

`B. \(a = -3\), \(b = -6\), \(c = 2\)`

`C. \(a = -3\), \(b = -6\), \(c = -2\)`

`D. \(a = 3\), \(b = -6\), \(c = 2\)`

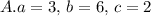
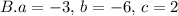
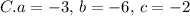
The vertex form of a quadratic function
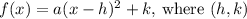`\(f(x) = a(x-h)^2 + k\), where \((h, k)\)` is the vertex of the parabola.

`A. \(f(x) = 3(x+1)^2 + 2\): The vertex is \((-1, 2)\).`

`B. \(f(x) = -3(x+1)^2 + 2\): The vertex is \((-1, 2)\).`

`C. \(f(x) = -3(x+1)^2 - 2\): The vertex is \((-1, -2)\).`

`D. \(f(x) = 3(x-1)^2 + 2\): The vertex is \((1, 2)\).`

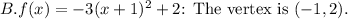
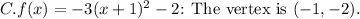
Therefore, based on the analysis of the vertex, the correct answer is: B:
`\(f(x) = -3(x+1)^2 + 2\).`