Question

What is the solution to the system of linear equations below? 2/5x−y=6 −2x+5y=−30 Select one: A. (-13, 14) B. (-5, -8) C. no solution D. infinitely many solutions

Answer 1

D. Infinitely many solutions

Explanation:

`-(2)/(5)x-y=6 | -2x+5y=-30`

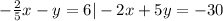
1.Since neither equation contains an isolated. However, we can isolate -y in the first equation by adding
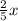`(2)/(5)x` to both sides.

Like this:
`(2)/(5)x-(2)/(5)x-y=6-(2)/(5)x`

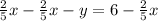
ending up with
`y=6-(2)/(5)x`

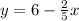
2.Now, we can change y to a positive y. By doing so, we divide -y by the entire equation.

Like this
`(-y=6-(2)/(5)x )/(-y)`

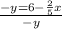
Ending with
`y=-6+(2)/(5)x`

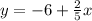
3.Now, we can plug the expression
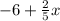`-6+(2)/(5)x` into the second equation as a substitute for y, and solve for x. Then, we can use x to calculate y.

Like this
`-2x+5(-6+(2)/(5)x)=-30\\ -2x-30+2x=-30\\`

4. Since -2x+2x would cancel out and leave -30=-30. This is true because we know -30 equals -30 with no variable in sight.