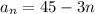Answer:
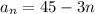
Explanation:
Method 1:
Arithmetic sequence is in the form
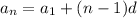
d is the common difference, can be found by:
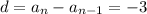
Subtituting the
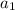 and
and
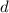
You get:

Method 2 (Mathematical induction):
Assume it is in form
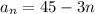
Base step:
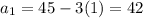
Inducive hypophesis:
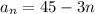
GIven:
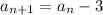
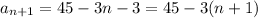
Proved by mathematical induction