Answer:
Step-by-step explanation:
We need to find the x-components of each of these vectors and then add them together, then we need to find the y-components of these vectors and then add them together. Let's get to that point first. That's hard enough for step 1, dontcha think?
The x-components are found by multiplying the magnitude of the vectors by the cosine of their respective angles, while the y components are found by multiplying the magnitude of the vectors by the sine of their respective angles.
Let's do the x-components for all the vectors first, so we get the x-component of the resultant vector:
 and
and
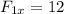
 and
and
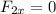
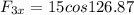 and
and
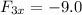 (the angle of 126.87 is found by subtracting the 53.13 from 180, since angles are to be measured from the positive axis in a counterclockwise fashion).
(the angle of 126.87 is found by subtracting the 53.13 from 180, since angles are to be measured from the positive axis in a counterclockwise fashion).
That means that the x-component of the resultant vector, R, is 3.0
Now for the y-components:
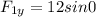 and
and
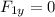
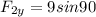 and
and
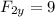
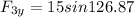 and
and
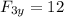
That means that the y-component of the resultant vector, R, is 21.
Put them together in this way to find the resultant magnitude:
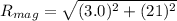 which gives us
which gives us
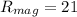 and now for the angle. Since both the x and y components of the resultant vector are positive, our angle will be where the x and y values are both positive in the x/y coordinate plane, which is Q1.
and now for the angle. Since both the x and y components of the resultant vector are positive, our angle will be where the x and y values are both positive in the x/y coordinate plane, which is Q1.
The angle, then:
 degrees, and since we are QI, we do not add anything to this angle to maintain its accuracy.
degrees, and since we are QI, we do not add anything to this angle to maintain its accuracy.
To sum up: The resultant vector has a magnitude of 21 N at 82°