Question

Anyone know how to do this

Answer 1

The area of the rectangle on the left side is

`9cm \: * 4cm = 36 {cm}^(2)`

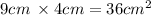
The area of the bottom rectangle is

`6cm * 2cm = 12 {cm}^(2)`

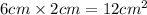
The total area of the composite figure will be

`36 {cm}^(2) + 12 {cm}^(2) = 48 {cm}^(2)`

Explanation:

The area of any given rectangle can be found by multiplying the length of that rectangle by its width. The rectangle on the left side has a length of 9cm but the width is unknown. To find the width, we subtract 6cm from the width of the bottom rectangle: 10cm. And that gives us 4cm.

Therefore, we can now calculate the area to be: length × width = 9cm × 4cm = 36cm²//

The area of the bottom rectangle can be found similarly by multiplying the length: 2cm by the width: 6cm of that rectangle. And the result gives us: 2cm × 6cm = 12cm²//

The total area of the composite figure is calculated by adding the results from the left and bottom rectangles together. And that gives us: 36cm² + 12cm² = 48cm²//