Question

Express each of the following in the form


`{7}^(x)`
a)

`\sqrt[5]{7}`
b)

`\frac{1}{ \sqrt[7]{7} }`
Answer:

Explanation:​

Answer 1

Answers:

• a)
  `7^(1/5)`
• b)
  `7^(-1/7)`

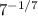
Each answer has 7 as the base and a fraction as an exponent.

==========================================================

Step-by-step explanation:

One useful rule here is that
`\sqrt[n]{x^m} = x^(m/n)`. The fraction m/n is the exponent for the base x. Note how the index of the root (n) becomes the denominator of the fraction m/n. So for example if we had n = 3, then we'd be dealing with a cube root.

For part a), we have x = 7, m = 1 and n = 5 to get

`\sqrt[n]{x^m}=x^(m/n)\\\\\sqrt[5]{7^1}=7^(1/5)\\\\\sqrt[5]{7}=7^(1/5)\\\\`

-----------------

Part b) is the same idea

We would find that

`\sqrt[n]{x^m}=x^(m/n)\\\\\sqrt[7]{7^1}=7^(1/7)\\\\\sqrt[7]{7}=7^(1/7)\\\\`

Then apply the reciprocal to both sides. This is the same as raising both sides to the exponent -1

`\sqrt[7]{7}=7^(1/7)\\\\\left(\sqrt[7]{7}\right)^(-1)=\left(7^(1/7)\right)^(-1)\\\\\frac{1}{\sqrt[7]{7}}=7^(1/7*(-1))\\\\\frac{1}{\sqrt[7]{7}}=7^(-1/7)\\\\`

You could also use the rule that x^(-y) = 1/(x^y) when dealing with negative exponents.

In the second to last step shown above, I used the rule (x^y)^z = x^(y*z) on the right hand side.