Question

a car of mass 500 kg travelling with a speed of 54km/hr is brought to rest over a distance of 40 m. find the acceleration and force applied on brakes​

Answer 1

Step-by-step explanation:

`a=(v_f-v_0)/(t)` We don't yet need the mass of the car, as we can see by this equation. What we do need is the velocity of the car, the initial velocity, in meters per second, and right now it's in km/hr. Not good. We need to convert. The conversion is as follows:

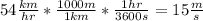`54(km)/(hr)*(1000m)/(1km)*(1hr)/(3600s)=15(m)/(s)` Ok, that's good. Now we have everything we need but the time element. If the car traveled a distance of 40 meters at 15 m/s, then we can use the d = rt equation to solve for t, and when we find t we plug it into the acceleration equation:

40 = 15t and

t = 2.7 seconds. The car traveled for 2.7 seconds to go that 40 meters. That's the only reason we were given the displacement. We need it for nothing else but that.

Filling in the acceleration equation now:

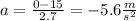`a=(0-15)/(2.7)=-5.6(m)/(s^2)` and the negative indicates we are in fact slowing down. That's the answer for the acceleration portion of the problem; now we need the force, F, applied to the brakes.

F = ma where m is mass (we get to use that value now!) and a is -5.6 m/s/s.

F = 500(-5.6) and

F = -2800 N and the negative here means that the force of the brakes is acting against the motion of the car: the brakes are pulling the car "backwards" to stop while the car's motion is forward. The negative indicates the direction the force is being applied.