Question

Let X be a random variable with density function f(x) = 2e^−2x
Calculate P( X≤ 0.5| X≤ 1)

Answer 1

By definition of conditional probability,

P(X ≤ 0.5 | X ≤ 1) = P((X ≤ 0.5) and (X ≤ 1)) / P(X ≤ 1)

but if X ≤ 0.5, then it's automatic that X ≤ 1, so

P(X ≤ 0.5 | X ≤ 1) = P(X ≤ 0.5) / P(X ≤ 1)

Given the PDF of X,

`f_X(x) = \begin{cases}2e^(-2x)&\text{if }x\ge0\\0&\text{otherwise}\end{cases}`

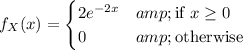
the CDF would be

`P(X\le x) = F_X(x) = \displaystyle\int_(-\infty)^x f_X(t)\,\mathrm dt`

`F_X(x) = \begin{cases}0&\text{if }x<0\\1-e^(-2x)&\text{if }x\ge0\end{cases}`

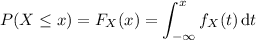
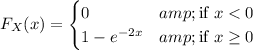
So we have

P(X ≤ 0.5 | X ≤ 1) = (1 - exp(-2 × 0.5)) / (1 - exp(-2 × 1))

… = (1 - exp(-1)) / (1 - exp(-2))

… = (1 - 1/e) / (1 - 1/e ²)

… = (e ² - e) / (e ² - 1)

… = e / (e + 1) ≈ 0.7312