By definition of conditional probability,
P(X ≤ 0.5 | X ≤ 1) = P((X ≤ 0.5) and (X ≤ 1)) / P(X ≤ 1)
but if X ≤ 0.5, then it's automatic that X ≤ 1, so
P(X ≤ 0.5 | X ≤ 1) = P(X ≤ 0.5) / P(X ≤ 1)
Given the PDF of X,
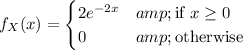
the CDF would be
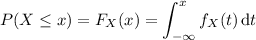
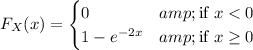
So we have
P(X ≤ 0.5 | X ≤ 1) = (1 - exp(-2 × 0.5)) / (1 - exp(-2 × 1))
… = (1 - exp(-1)) / (1 - exp(-2))
… = (1 - 1/e) / (1 - 1/e ²)
… = (e ² - e) / (e ² - 1)
… = e / (e + 1) ≈ 0.7312