Answer:
Assume that
 , and that the air resistance on the stone is negligible.
, and that the air resistance on the stone is negligible.
a.
Height of the stone:
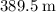 (above the ground.)
(above the ground.)
Velocity of the stone:
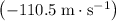 (the stone is travelling downwards.)
(the stone is travelling downwards.)
b.
Height of the stone:
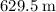 (above the ground.)
(above the ground.)
Velocity of the stone:
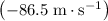 (the stone is travelling downwards.)
(the stone is travelling downwards.)
Step-by-step explanation:
If air resistance on the stone is negligible, the stone would be accelerating downwards at a constant
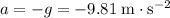 .
.
Let
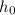 denote the initial height of the stone (height of the stone at
denote the initial height of the stone (height of the stone at
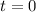 .)
.)
Similarly, let
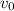 denote the initial velocity of the stone.
denote the initial velocity of the stone.
Before the stone reaches the ground, the height
 (in meters) of the stone at time
(in meters) of the stone at time
 (in seconds) would be:
(in seconds) would be:
 .
.
Similarly, before the stone reaches the ground, the velocity
 (in meters-per-second) of the stone at time
(in meters-per-second) of the stone at time
 (in seconds) would be:
(in seconds) would be:
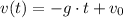 .
.
In section a.,
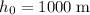 while
while
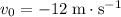 (the stone is initially travelling downwards.) Evaluate both
(the stone is initially travelling downwards.) Evaluate both
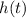 and
and
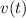 for
for
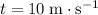 :
:
![\begin{aligned} h(t) &= -(1)/(2)\, g \cdot t^(2) + v_0 \cdot t + h_0 \\ &= -(1)/(2)\ * 9.81\; \rm m\cdot s^(-2)* (10\; \rm s)^(2) \\&\quad\quad + \left(-12\; \rm m \cdot s^(-1)\right) * 10\; \rm s + 1000\; \rm m \\[0.5em] &= 389.5\; \rm m \end{aligned}](https://img.qammunity.org/2022/formulas/physics/high-school/hd9s3c9h0nlll5zeeokuyfcsq5rsoq7l8f.png) .
.
Indeed, the value of
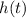 at
at
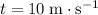 is greater than zero. The stone hasn't yet hit the ground, and both the representation for the height of the stone and that for the velocity of the stone are valid.
is greater than zero. The stone hasn't yet hit the ground, and both the representation for the height of the stone and that for the velocity of the stone are valid.
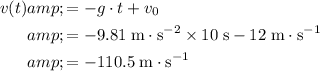 .
.
The value of
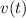 at
at
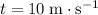 is negative, meaning that the stone would be travelling downwards at that time.
is negative, meaning that the stone would be travelling downwards at that time.
In section b.,
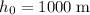 while
while
 (the stone is initially travelling upwards.) Evaluate both
(the stone is initially travelling upwards.) Evaluate both
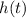 and
and
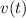 for
for
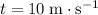 :
:
![\begin{aligned} h(t) &= -(1)/(2)\, g \cdot t^(2) + v_0 \cdot t + h_0 \\ &= -(1)/(2)\ * 9.81\; \rm m\cdot s^(-2)* (10\; \rm s)^(2) \\&\quad\quad + 12\; \rm m \cdot s^(-1) * 10\; \rm s + 1000\; \rm m \\[0.5em] &= 629.5\; \rm m \end{aligned}](https://img.qammunity.org/2022/formulas/physics/high-school/6xui5456v6l7kvosiqw2k8v9zd5b0tt8an.png) .
.
Verify that the value of
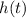 at
at
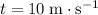 is indeed greater than zero.
is indeed greater than zero.
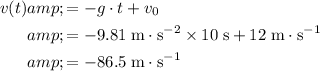 .
.
Similarly, the value of
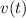 at
at
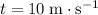 is negative because the stone would be travelling downwards at that time.
is negative because the stone would be travelling downwards at that time.