Question

The diagram shows the sector of a circle with the centre O and radius 6cm.

MN is a chord of the angle.
angle MON is 50 degrees

calculate the area of the shaded segment
give your answer to 3 significant figures

Answer 1

Area of the shaded region = 1.92 cm²

Explanation:

From the picture attached,

Area of the shaded region = Area of the sector OMN - Area of the triangle OMN

Area of sector OMN =
`(\theta)/(360)(\pi r^(2))`

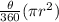
Here, θ = Central angle of the sector

r = radius of the sector

Area of sector OMN =
`(50)/(360)(\pi )(6)^2`

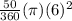
= 15.708 square cm

Area of ΔOMN = 2(ΔOPN)

Area of ΔOPN =
`(1)/(2)(OP)(PN)`

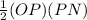
Area of ΔOMN = OP × PN

In ΔOPN,

sin(25°) =
`(PN)/(ON)`

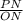
PN = ONsin(25°)

= 6sin(25°)

= 2.536 cm²

cos(25°) =
`(OP)/(ON)`

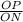
OP = ONcos(25°)

OP = 6cos(25°)

OP = 5.438 cm

Area of ΔOMN = 2.536 × 5.438

= 13.791 cm²

Area of the shaded region = 15.708 - 13.791 = 1.917 cm²

≈ 1.92 cm²