Question

Work out area of ABCD

Answer 1

Area of ABCD = 45.1 cm²

Explanation:

From the figure attached,

Area of ABCD = Area of ΔBCD + Area of ΔABD

Area of ΔABD =
`(1)/(2)(AB)(BD)`

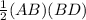
sin(55°) =
`\frac{\text{Opposite side}}{\text{Hypotenuse}}`

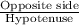
sin(55°) =
`(AB)/(BD)`

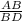
AB = 10sin(55°)

AB = 8.19 cm

cos(55°) =
`\frac{\text{Adjacent side}}{\text{Hypotenuse}}`

=
`(AD)/(BD)`

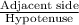
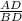
AD = 10cos(55°)

AD = 5.74cm

Area of ΔABD =
`(1)/(2)(8.19)(5.74)`

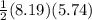
= 23.51 cm²

Area of ΔBCD =
`(1)/(2)(\text{Base})(\text{Height})`

=
`(1)/(2)(BD)(CE)`

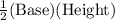
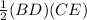
tan(38°) =
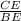
`(CE)/(BE)`

BE =
`\frac{CE}{\text{tan}(38)}`

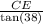
Similarly, DE =
`\frac{CE}{\text{tan}(44)}`

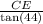
Since, BE + DE = 10 cm

`\frac{CE}{\text{tan}(38)}+\frac{CE}{\text{tan}(44)}=10`

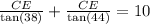
CE(1.28 + 1.04) = 10

CE(2.32) = 10

CE = 4.31 cm

Area of ΔBCD =
`(1)/(2)(10)(4.31)`

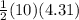
= 21.55 cm²

Area of ABCD = Area of ΔBCD + Area of ΔABD

= 21.55 + 23.51

= 45.06

≈ 45.1 cm²