Answer:
Therefore, the gravitational zero points between two planetoids lie at a distance of 3000 m from the center of planetoid 1.
Step-by-step explanation:
From Newton’s gravitation formula, the expression of the mass (M) of the planet of radius R is given as,
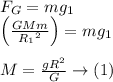
Let's take x to be the distance of the zero gravitational points from the center of the planetoid 1.
Thus, the distance of the zero gravitational points from the center of the planetoid 2 is (D-x).
At zero gravitational point, the gravitational force between the planets and the rocket must be equal.