Question

C. Find the mean, variance and standard deviation of the following probability distributions. (5 pts.) X 1 6 11 16 21 P(X) 1/7 1/7 2/7 1/7 277 D. Given the population of 5,000 scores with p = 86 and o = 10. How many scores are; (10 pts.) A Between 96 to 1067 B. middle 50% of the distribution? E. How many different samples of size n = 3 can be selected from a population with the following sizes? (5pts)

​

Answer 1

(C) You're given a probability mass function,

`P(X=x)=\begin{cases}\frac17&\text{if }x\in\{1,6,16\}\\\frac27&\text{if }x\in\{11,21\}\\0&\text{otherwise}\end{cases}`

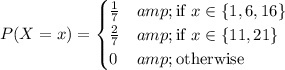
The mean is

`\displaystyle E[X] = \sum_x x\,P(X=x) = \frac{1*1}7 + \frac{1*6}7 + \frac{1*16}7 + \frac{2*11}7 + \frac{2*21}7 = \boxed{\frac{87}7} \approx 12.43`

The variance is

`\displaystyle V[X] = \sum_x x^2\,P(X=x) = \frac{1^2}7 + \frac{6^2}7 + \frac{16^2}7 + \frac{2*11^2}7 + \frac{2*21^2}7 = \boxed{\frac{1417}7} \approx 202.43`

The standard deviation is simply the square root of the variance:

`√(V[X]) = \boxed{\sqrt{\frac{1417}7}} \approx 14.23`

(D) I'm not entirely sure what is being asked here, so I'm kinda guessing at the meaning. I think the question is saying there is a large set of 5000 test scores that are normally distributed with mean µ = 86 and standard deviation σ = 10.

Let X be the random variable representing these test scores. Then

(D.A)

`P(96 < X < 106) = P\left((96-86)/(10) < (X-86)/(10) < (106-86)/(10)\right) = P(1 < Z < 2)`

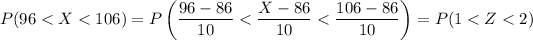
where Z follows the standard normal distribution with mean 0 and variance 1.

To find the remaining probability, you can use the empirical rule (68/95/99.7) which says

• approximately 68% of a normal distribution lies within 1 standard deviation of the mean; in other words,
`P(-1<Z<1)\approx0.68`

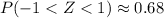
• approximately 95% of the distribution lies within 2 standard deviations;
`P(-2<Z<2)\approx0.95`

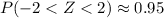
The normal distribution is also symmetric about its mean. Taking these facts together, we find

`P(1<Z<2) = \frac{P((-2<Z<-1)\text{ or }(1<Z<2))}2 = \frac{P(-2<Z<2)-P(-1<Z<1)}2 \approx 0.135`

So roughly 13.5% of all test scores will fall between 96 and 106, and 13.5% of 5000 is 675. (The actual probability is closer 0.135905, and the projected test score count is closer to 679.)

(D.B) Any 50% of the distribution is still 50% of the distribution, so half of all the test scores would fall in this range. There would be 2500 test scores in that group.

(E) No choices given here...