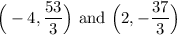Answer:
Part A)
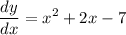
Part B)
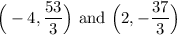
Explanation:
We are given the function:
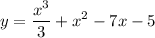
Part A)
To find dy/dx, differentiate both sides with respect to x:
![\displaystyle (dy)/(dx)=(d)/(dx)\Big[(x^3)/(3)+x^2-7x-5\Big]](https://img.qammunity.org/2022/formulas/mathematics/college/klfjn1shnhq315zwh5huug3n5y7x4sygw1.png)
Differentiate:
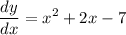
Part B)
We want the points on the curve where the gradient is parallel to y = x.
The equation y = x has a constant gradient of 1.
Therefore, we can set dy/dx = 1 and solve for x:
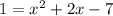
Rewrite:
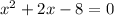
Factor:
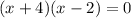
Thus:
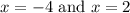
And substituting them back for the original equation, we acquire:
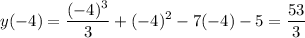
And:
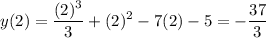
Our points are: